A Verifiable Distributed Voting System without a Trusted Party
Summary by Daniel Grossman
Overview
Elections enable individuals to express their thoughts and opinions without compromising privacy. Maintaining voter confidentiality is an essential component of elections – no one party should be able to link the vote to the voter. However, typical voting systems today have limitations, in particular the need for trusting a third party with voter privacy. While certain decentralized voting systems have attempted to solve this problem, none can handle attacks from within the network. This paper provides a practical solution: a voting system that can “operate independently of any trusted party by distributing the vote administration to a number of voting authorities.”
Essential security properties
- Accuracy = It’s impossible for a valid vote to be altered or omitted from the final tally.
- Conversely, it’s impossible for an invalid vote to be counted.
- Privacy = A vote cannot be connected to the voter who submitted it (ie. zero-knowledge)
- Verifiability = Anyone can independently verify all votes have been correctly counted.
- Flexibility = The ballot can have different formats including write-ins.
- No trusted party = The properties of the voting scheme are guaranteed to hold even if one or multiple parties, up to a threshold, are compromised. In other words, a majority of voting authorities complying with the scheme is necessary (51%+). This is no different than other distributed networks like Bitcoin or Ethereum.
How it works
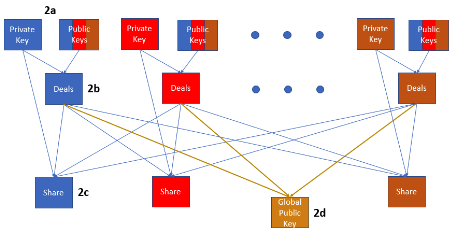
- Initialization = Each voter supplies a portion of a public key to the system ie. voting “authorities.”
- Communication = The voting authorities compute a global public key from all the voters’ portions.
- Vote collection = Any voter may submit a ballot encrypted with the newly created global key. The ballot will be linked to the voter for verification purposes, but the vote will not.
- Flexibility = Once all the ballots are submitted, they’re shuffled in a publicly verifiable but untraceable manner, obscuring the relationship between voter and ballot.
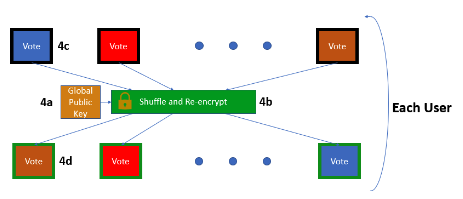
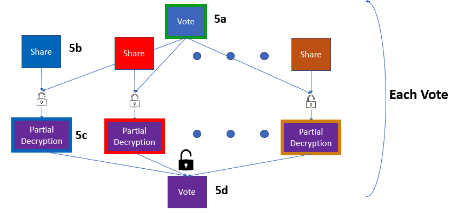
- Decryption = Each shuffled ballot is publicly decrypted in a joint computation. A threshold number of voters must all contribute for the ballot to be decrypted.
Implementation and Results
Real-world implementation was achieved with the production of several functions: one creating a public-private keypair for each voting authority, one publishing the global public key, one dealing private key shares to each authority, one decrypting votes using these shares, and one shuffling and verifying the votes.
Bouck executed several runtime tests to demonstrate the feasibility of this system, altering the number of voters, ballots and threshold of voters required for decryption. Because the voting scheme setup (the “initialization” and “communication” phases) took longer than the other stages, runtime here was averaged over ten trials. For all other election phases, the runtime was averaged over fifty trials.
The runtime of the vote collection, shuffle, and decryption stages generally produced a linear function with respect to the number of ballots and voting authorities. In other words, the greater the number of ballots and voting authorities, the longer the election took to complete. However, even with the maximum number of ballots (1024), the runtimes for each function still only took about ten seconds maximum.
Implications
This system is completely distributed while accomplishing secure, private voting: dozens of authorities could run elections for thousands of voters without a trusted central jurisdiction. Such a scheme could vastly improve our democratic institutions; there is no third party or central authority able to control or alter electoral results. In politically unstable countries with corrupt democracies, this system could provide strong verification and legitimacy for elections. It also opens the door for any person, organization or institution to run a secure, decentralized election, simultaneously increasing democracy’s accessibility while decreasing cost.
A weakness of this system is that it assumes a majority of users will not collude or deviate from the scheme. Nevertheless, as long as there is a majority of legitimate operators, the election will remain secure. Voters can also modify their votes until the result is revealed. While this might not seem ideal, it does prevent a premature reveal of votes which could influence election results. Lastly, shuffles could be more efficiently designated to certain voting authorities instead of the entire set, ultimately reducing computation time.